目次
記号の定義
前進偏差分演算子\(\frac{\eth }{\eth \bullet}\)と後進偏差分演算子\(\frac{\eth }{\eth \bullet}\)を以下のように定義する $$\frac{\eth u}{\eth x}:=\frac{u(x+\varDelta x,t)-u(x,t)}{\varDelta x}$$ $$\frac{\eth u}{\eth t}:=\frac{u(x,t+\varDelta t)-u(x,t)}{\varDelta t}$$ $$\frac{u\eth}{\eth x}:=\frac{u(x,t)-u(x-\varDelta x,t)}{\varDelta x}$$ $$\frac{u\eth}{\eth t}:=\frac{u(x,t)-u(x,t-\varDelta t)}{\varDelta t}$$1.差分法による拡散方程式の数値解
以下に示す拡散方程式\((1.1)\)を差分化して\(u(x,t)\)の数値解を求める。初期条件と境界条件は\((1.2),(1.3)\)とする。 $$\frac{\partial u}{\partial t}=\kappa\frac{\partial^2u}{{\partial x}^2}\tag{1.1}$$ $$\begin{rcases}u(0,t)=1\\u(1,t)=0\end{rcases}\tag{1.2}$$ $$\kappa=0.1\tag{1.3}$$ この式で表せるモデルは多数あるが、例えば長さ\(1\)で、左端の温度が常に\(1\)、右端の温度が常に\(0\)に調整されている、熱拡散率\(\kappa\)の金属棒の温度分布などが挙げられる。
\((1.1)\)の微分演算子を $$\frac{\partial^2\bullet}{{\partial x}^2}\to\frac{\frac{\eth\bullet}{{\eth x}}\eth}{{\eth x}},\ \frac{\partial}{\partial t}\to\frac{\eth}{\eth t}$$ と置き換えて差分化すると、1) $$\begin{align*}&\frac{\eth u}{\eth t}=|c|^2\frac{\eth^2u}{{\eth x}^2}\\&\iff u(x,t+\varDelta t)-u(x,t)=\kappa\frac{\varDelta t}{{\varDelta x}^2}(u(x+\varDelta x,t)-2u(x,t)+u(x-\varDelta x,t))\\&\iff u(x,t+\varDelta t)=\alpha u(x+\varDelta x,t)+(1-2\alpha)u(x,t)+\alpha u(x-\varDelta x,t)\tag{1.4}\end{align*}$$2) となる。
式\((1.2)\)~式\((1.4)\)をprogramに落とし込めば、\(u\)の数値解が求まる。 今回は、\(\varDelta x=0.05,\varDelta t=0.01\)での\(t=0,25,50,75,100\)における\(u\)の分布図を画像で出力するprogramをpythonで作成し、結果を得た。 図表出力にはmatplotlibを使った。
programを図1.2に、プログラムの変数と式(1.2)~(1.4)中の変数の対応表を表1.1に示す。
#
# 差分法の計算例
#
import numpy as np
import matplotlib.pyplot as plt
# 入力データ
kappa = 0.1
t_step = 100
n_step=20
x_len = 1.
dt = 0.01
u = np.zeros((t_step+1)*(n_step+1)).reshape (t_step+1, n_step+1)
x = np.linspace(0., x_len, n_step+1)
#境界条件
for j in range(0, t_step+1):
u[j][0] = 1
# 差分法
dx = x_len/n_step
alp = kappa*dt/(dx*dx)
if alp>0.5:
print("alp < 0.5となるように設定して下さい!")
else:
for j in range(0, t_step):
for i in range (1, n_step):
u[j+1][i] = alp*u[j][i+1] + (1-2*alp)*u[j][i] + alp*u[j][i-1]
plt.plot(x, u[0])
plt.plot(x, u [25])
plt.plot(x, u[50])
plt.plot(x, u[75])
plt.plot(x, u[100])
main.pyを実行して生成したグラフを図1.3に示す
main.pyの実行結果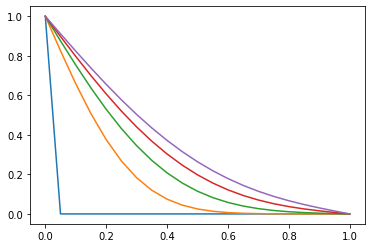
| 色 | \(t\) |
|---|---|
| 青 | 0 |
| 橙 | 25 |
| 緑 | 50 |
| 赤 | 75 |
| 紫 | 100 |
2.動的なレポートシステムの提案
ここでは、従来の静止画的表現にとらわれない研究の表現を追求するために、HTMLで論文やレポートを記述することを提案する。
HTML(とJS)ならではの表現方法として、実行環境を用意する事なく、レポート上で直接数値解析を行なえるUXを実装する。ここでは、レポート上でリアルタイムにパラメタを調節して前章の偏微分方程式の数値解をプロットするプログラムを提示する。 グラフ下部にある3つのスライダを操作すると、対応する数値解がリアルタイムにグラフに反映される。また差分法の収束条件\(\alpha<\frac12\)から外れると警告メッセージが表示されるようプログラムされている codingにはJavascriptを用いた。ソースコードはここから取得できる
この手法は紙媒体ではできない、デジタル媒体独自の情報表現手法ではある。しかし、この手法はインターネット上でよく見かける手法3)であり、新奇性に乏しい。また確かに紙媒体やPDF、WORDでは難しい表現ではあるが、論文で使えたら便利な場面はあまり思い当たらない そのため、論文でも活用できるようなHTML+JS独自の表現方法を提示できれば、より説得力のある内容になったかも知れない。
そのようなHTML+JS独自の表現方法として、例えば以下のような手法がある。
2.1.レポート上で動く数値解析プログラム
これらをこのレポート上で示せなかったのは筆者の実装力が不足していた点であり、今後の改善点だと考える。
例:ノモンハン 大戦の起点と終止符 - プレミアムA:朝日新聞デジタル